Sơ đồ tư duy hệ thức lượng trong tam giác

Sơ đồ tư duy hệ thức lượng trong tam giác trực quan, dễ nhớ nhất giúp các bạn học sinh nắm được kiến thức qua phương pháp học tập bằng mindmap.

Sơ đồ tư duy hệ thức lượng trong tam giác

Mẫu 1

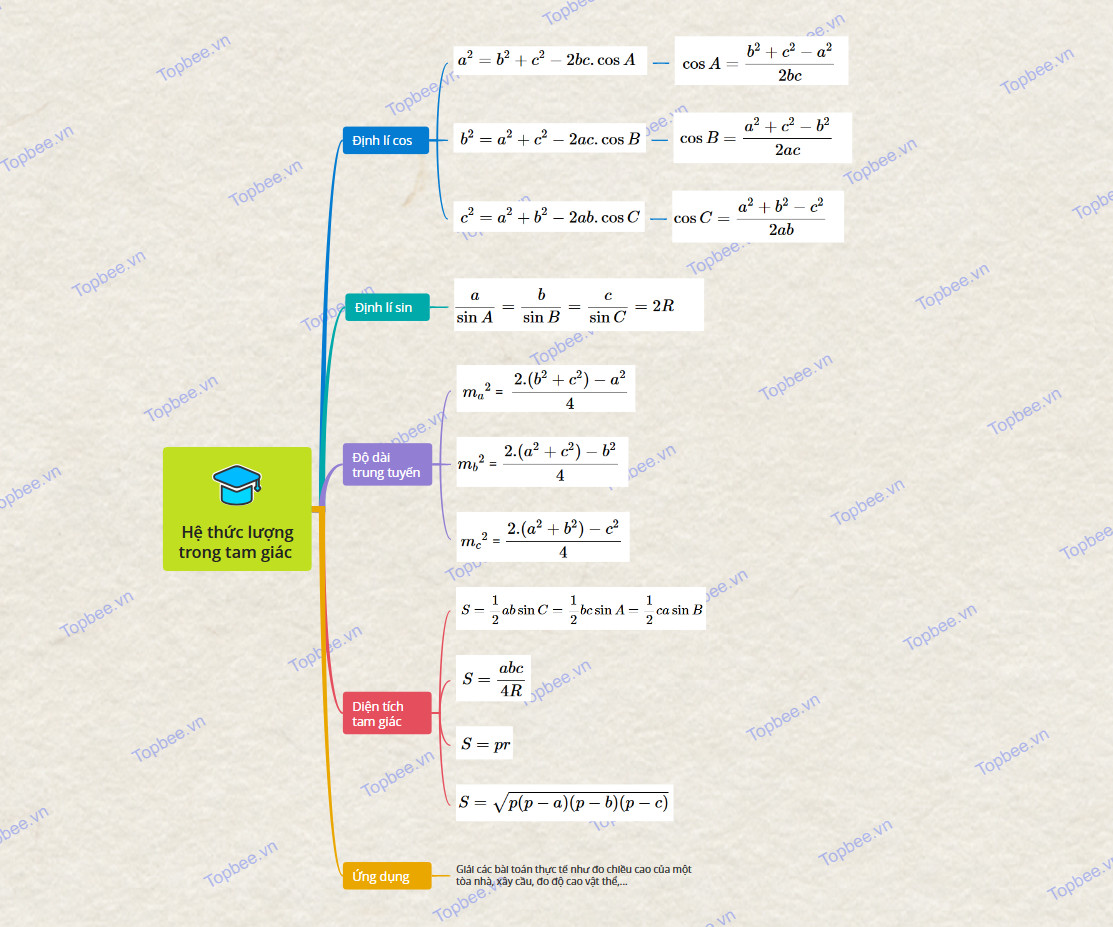
Mẫu 2

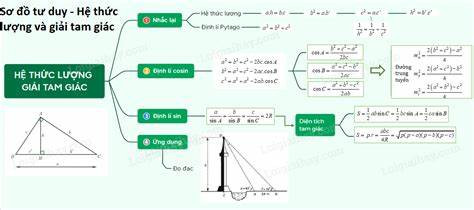
Mẫu 3

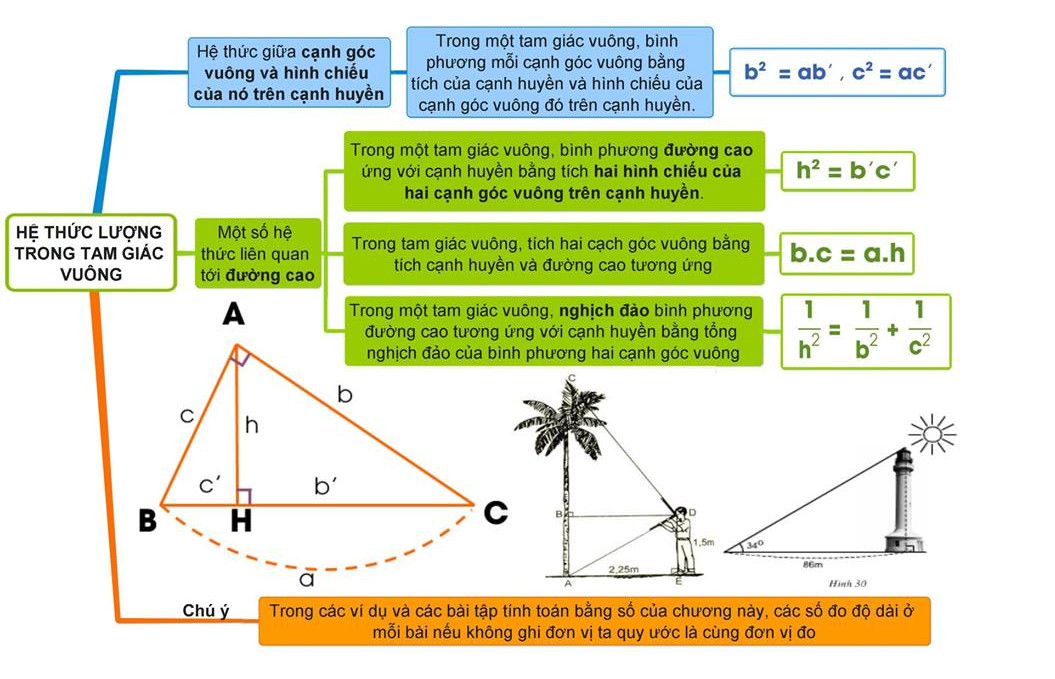
Mẫu 4

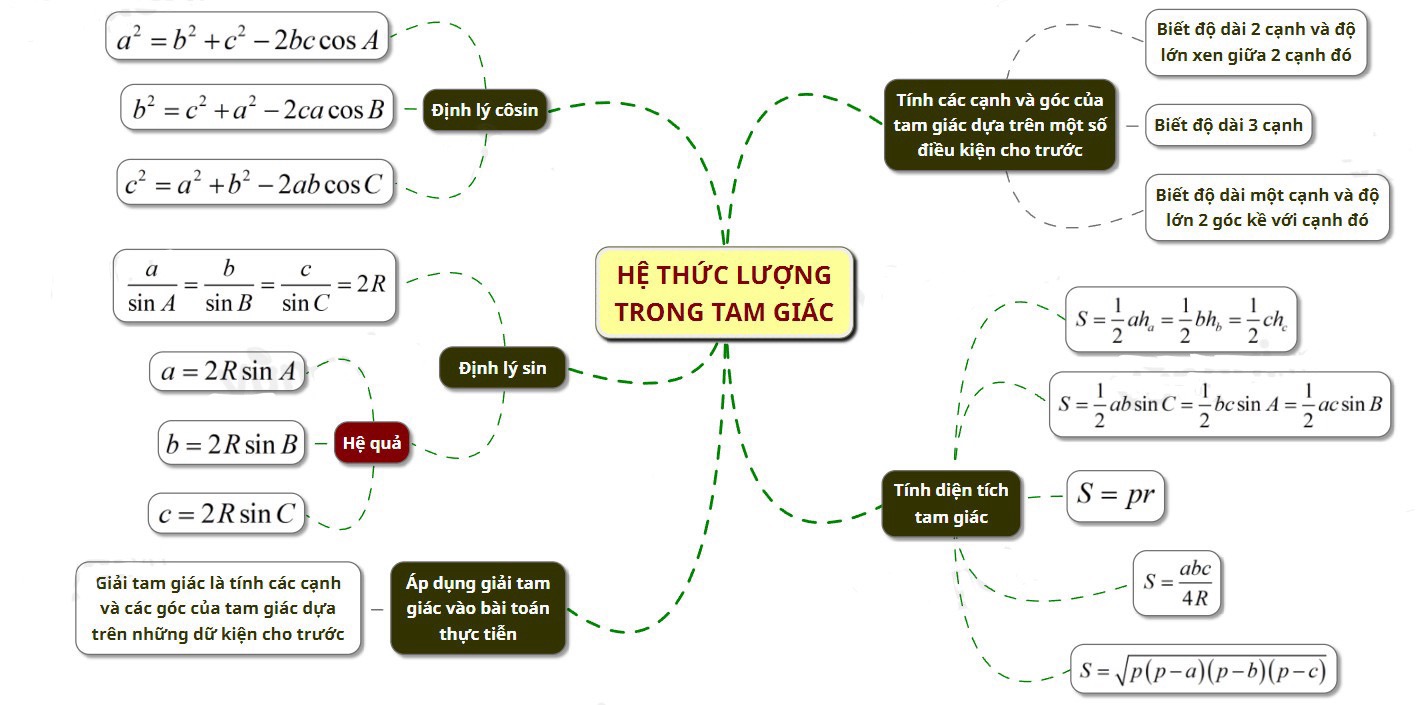
Các câu hỏi vận dụng về hệ thức lượng trong tam giác

Câu 1: Cho ΔABC có AB = 6, AC = 8, góc A = 120⁰

a. Tính diện tích ΔABC

b. Tính cạnh BC và bán kính đường tròn ngoại tiếp của tam giác ABC

*Lời giải:

a. Diện tích tam giác ABC

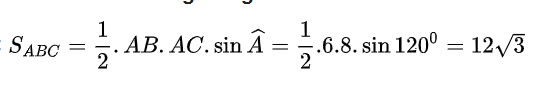
b. Theo bài ra ta có:

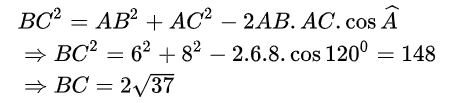
Vậy bán kính đường tròn ngoại tiếp tam giác ABC:

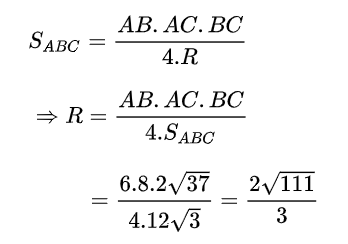
Câu 2: Cho tam giác ABC có AB = 1cm , AC = 2cm và góc A= 120⁰ . Tính BC.

*Lời giải:

Áp dụng định lí cosin ta có: 

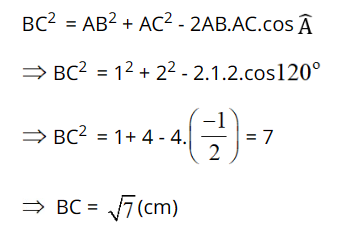
Câu 3: Tam giác ABC có AC = 3√3, AB = 3, BC = 6. Tính số đo góc B

A. 60°

B. 45°

C. 30°

D. 120°

*Lời giải: 

Áp dụng hệ quả của định lý côsin, ta có:

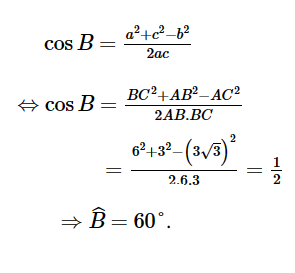
Chọn ý 

Câu 4: Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng

A. 1 cm;

B. √2cm;

C. 2 cm;

D. 3 cm.

*Lời giải:

Ta có AC= √ BC² - AB² = 8 cm

Diện tích tam giác ABC là: S = ½ AB.AC = 24 cm²

Nửa chu vi p=6+8+10 / 2 = 12 cm

Vậy: r = S / p= 24 / 12 = 2 cm

Chọn ý C.

Câu 5:  Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.

A. √43

B. 2√13

C. 8

D. 8√3

*Lời giải:

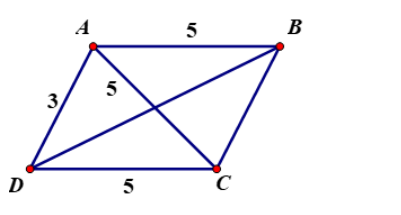
Gọi hình bình hành là ABCD, AD = 3, AB = 5

Gọi α là góc đối diện với đường chéo có độ dài 5

Ta có: 

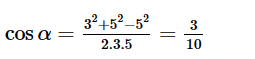
=> α là góc nhọn

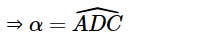
⇒ AC = 5

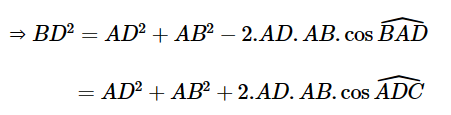
Thay số vào công thức ta có:

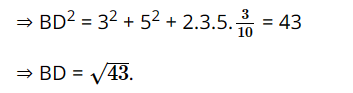
Chọn ý A.