Cho tam giác ABC vuông tại A, có AB = 9cm, BC = 15cm, AC =12 cm.a) So sánh các góc của tam giác ABC.b)Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD.

Cho tam giác ABC vuông tại A, có AB = 9cm, BC = 15cm, AC =12 cm.
a) So sánh các góc của tam giác ABC.
b)Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Chứng minh
từ đó suy ra tam giác BCD cân.
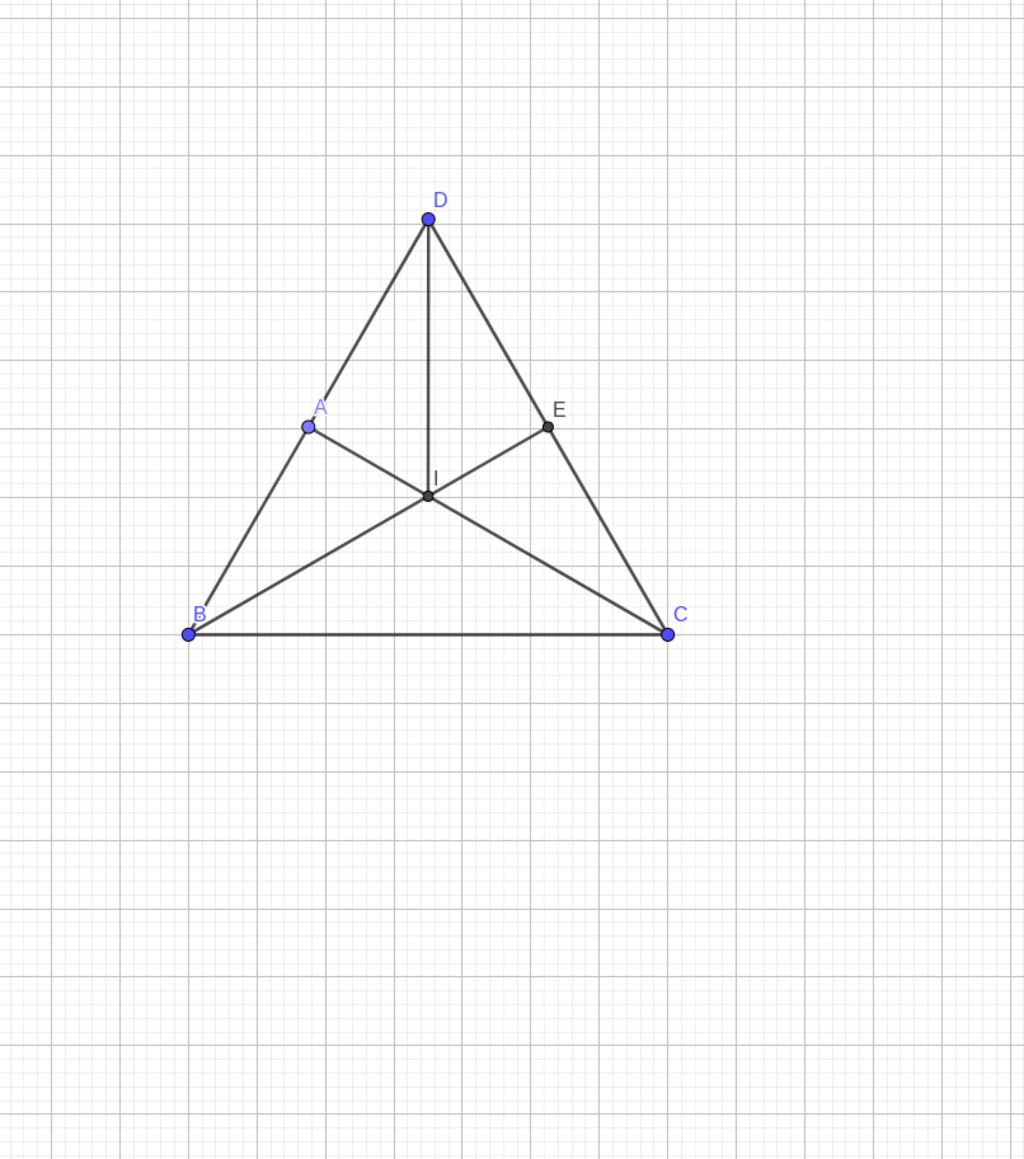
c) E là trung điểm cạnh CD, BE cắt AC ở I. Chứng minh DI đi qua trung điểm cạnh BC.